Logistic Regression
什么是分类问题
- 预测的变量是离散的值,例如:正例1,反例0
- 算法输出的边界在0~1之间
假设函数的选择
- 常用的Sigmoid Function函数: 。
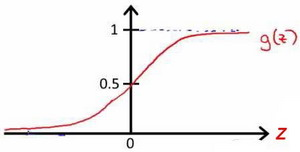
-
判断边界,根据不同的模型拟合不同的边界
-
边界为线性函数
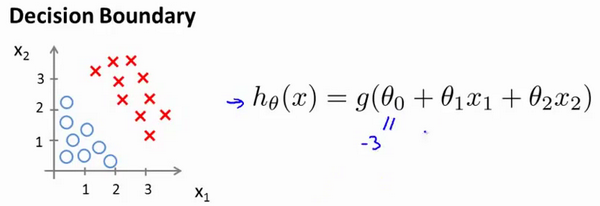
-
边界为多项式函数
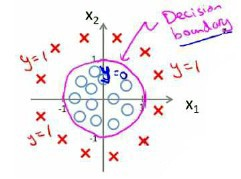
-
-
Sigmoid + 合适的边界函数 = 假设函数

代价函数
-
逻辑回归的拟合问题:由于我们选择的假设函数是Sigmoid函数,将其带入到线性回归的代价函数中,我们发现:我们得到的代价函数是一个具有多个局部最小值的函数,即非凸函数,这将影响到梯度下降法寻找全局最小值。

-
代价函数的选择:
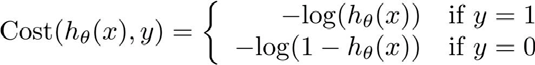
- 当实际值为1:若的值也为1,那么误差为0;反之,若距离1越远,误差越大
- 当实际值为0:若为0,那么误差也为0;反之,若距离0越远,那么输出的误差也就越大。
-
代价函数的化简:
将构建的 简化如下:
带入代价函数得到: 即:
-
代价函数为凸函数的推导:
可以看到,经过一连串的求导之后,我们得到了与线性回归同样的结果,但这并不意味着两者之间存在必然的关系。此外,除了梯度下降之外,还有一些优化的算法,这些算法比梯度下降更为高效:共轭梯度(Conjugate Gradient),局部优化法(Broyden fletcher goldfarb shann,BFGS)和有限内存局部优化法(LBFGS) (浅浅的埋个坑)
多类别分类
转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论,也可以邮件至 2542608082@qq.com